
| http://www.dontveter.com drt@christianliving.net, don@dontveter.com |
| Commercial Use Prohibited |
The algorithms in this chapter are methods that either are useful or have some potential for being useful or they are methods that have received a fair amount of attention for other reasons, however none of them has a direct bearing on the progress of the main ideas in the text, thus they can be studied or not studied as the reader desires.
A system closely related to the nearest neighbor classifier is the restricted Coulomb energy (RCE) network.1 The name is derived from an analogy with the electrostatic energy function governing the interactions of charged particles. The network works very much like the nearest neighbor algorithm except in order for an unknown point to be classified the same as its nearest neighbor it must be close enough to that neighbor. How close is close enough will vary from point to point. This distance limitation makes the RCE network more conservative than the nearest neighbor algorithm.

To illustrate the RCE learning algorithm we will work with the 12 non-linearly separable points in figure 3.4. The first point to add will be (13,1) and we do so by creating a middle layer unit with one connection to the A answer unit and connections to the two input units where the weights on these latter connections are just the coordinates of the point (13,1) with 13 for the x connection and 1 for the y connection. In addition we will start by assigning a close enough value to this unit of 3, so that if an unknown is within 3 units of this point it will be classified the same as this point, otherwise it will be unclassified. The network and its area of coverage is shown in figure 11.1.
Suppose we now want to add the point, (13,-1) to the network. First we calculate its distance to all its neighbors. Its only neighbor is only 2 units away from (13,1) and since it falls within the area of coverage of the point (13,1) we do not add this point to the network.
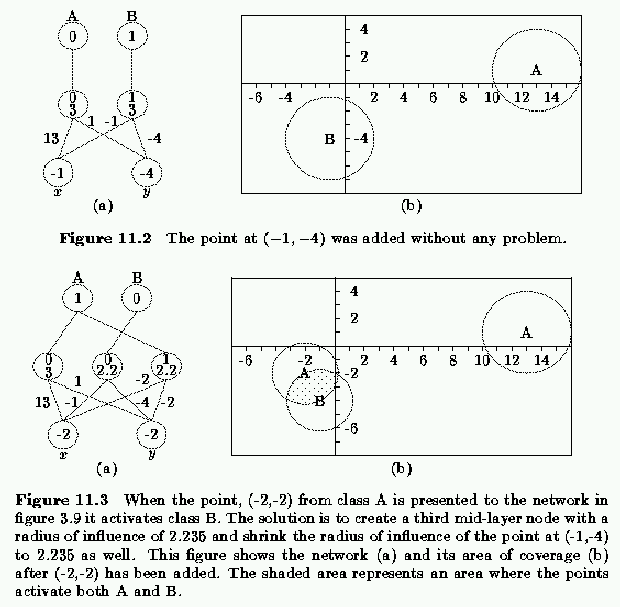
In another case we now add the point (-1,-4) to the network. It is not close enough to any other points and so it does not pose any added problems. A middle layer unit is added to store this point and an output layer unit is added to represent the class B. A single connection from the new middle layer unit to the new output unit is added. Its radius of coverage is also 3. The state of the network is now shown in figure 11.2. Adding the point (-2,-2) is more complicated. When it is presented to the network it activates the wrong answer, because it is only 2.236 units away from the point (-1,-4). In this case, a new midlayer unit needs to be created and wired in except its radius of influence must now be just under 2.236, say 2.235, in order to avoid conflict with the point (-1,-4). Also, because (-1,-4) responded to (-2,-2), its radius of influence must be decreased to 2.235. The new network and the division of the pattern space is shown in figure 11.3. There is still a large area between these two points that will be classified as both an A and a B. Further training with a large number of data points would be needed to develop an accurate boundary between the two classes. The division of the space using only the 12 data points is shown in figure 11.4.

RCE networks have the advantage that unknown points that are far from known data points get classified as unknown. For instance, if a network is looking at Social Security checks and one comes by for $1,000,286.23, the network, like a human being can warn that something is wrong because it has never seen a case like this before. On the negative side, unclassified points may result from just a simple gap that occurs between data points that are all of the same class. More sophisticated versions of the RCE network are described in [Reilly 1987] and [Collins 1988].

Another variation on pattern recognition networks is the so-called
higher-order type of network. In the networks we have looked
at so far the input to a unit has been in the form of:
|
| (11.1) |

Higher-order networks can also be trained using back-propagation [Rumelhart 1986] but the effect of using higher-order terms for input to a back-propagation network can also be duplicated in ordinary back-propagation networks. For instance in the XOR problem you can just supply a back-propagation network with the data, x1, x2 and x1x2. In this case, it turns out that a two-layer network is sufficient and the network also learns the patterns faster than a three-layer network. The arrangement is shown in figure 11.6.
This approach of using combinations of features obviously means that in large networks there will be a great many more weights in the polynomial but some researchers (for instance Maxwell et.al. [Maxwell 1986]) point out that it is not always necessary to include every possible pair of terms in the polynomial. If there is some information known about how features interact, possibly only a few extra terms need to be added to a linear polynomial and then the presence of these few extra terms can sometimes greatly reduce the training time.
Another important potential aspect of higher-order networks is that it seems as if it will be very convenient to actually implement them using optical technology where the weights are stored in a volume hologram (for instance see Psaltis et.al. [Psaltis 1986, 1987, 1988a, 1988b]). One report indicates that lithium niobate crystals could store over 109 connections per cubic centimeter. Clearly, optical evaluation of networks would be very fast. Optical systems that can learn the weights are being researched.
Most learning algorithms in this book have been of a type that uses supervised learning , training done by a teacher who gives the program the correct answer. In contrast to this, there is another type known as unsupervised learning . In unsupervised learning it is up to the system to try to divide its inputs into different categories, or clusters, without having any answers as to how the points should be classified. There are a great many clustering algorithms that have been devised but in this section we will only look at the simplest of them and in the following section we look at the ART1 program, which is a more complex clustering algorithm. Pattern recognition texts will contain many, many others.

As in supervised learning, the characteristics of a pattern are measured and written down as a vector. Suppose we have the data points as listed and plotted in figure 11.7 and we want a program to divide them up into different clusters, where each point in a cluster is close to the other points in the cluster. People would very likely divide these points into two clusters, once centered around (3,3) and another centered around (8,10). In the clustering algorithm we will give, a prototype point will develop near the center of each cluster. Each prototype point will be close to the average value of the coordinates of each point in the cluster.
To start the algorithm, there are no prototype points, so take the
first data point, d1 and set the first prototype point, p1 = d1. Now select a point, di from the data set and
find the distance from this point to every prototype point, where you
can define distance using any formula you want to. Here, we will just
use Euclidean distance. If the closest prototype point is close enough
to the data point (closeness is a parameter for the user to select),
then put the data point in the same category as this prototype point and
also modify the prototype point so that it is slightly closer to the
data point. If the closest prototype point is pc and it is
close enough to di then change pc as follows:
|


In addition to depending on the values of l and close enough, the order of presentation of the data points can affect the outcome. Cases can be constructed where the prototypes never settle down to stable positions. When more than one pass is made through the data set, a point may end up first in one cluster and later on in another. New clusters may be created in a later pass while old clusters can become unused. A common practice to stabilize the convergence is to slowly decrease l as time goes on.
Some results of using this algorithm with the 12 data points in figure 11.7 are shown in figures 11.8 and 11.9. In figure 11.8 the two clusters that resulted came from taking the maximum distance to be 5.0 with l = 0.2, 0.1 and 0.05 in three passes thru the data set while in figure 11.9, three clusters result when the distance is 4.0.
In addition to being used for machine classification, clustering can be applied separately to each class of a set of patterns used to train a back-propagation network in order to reduce the number of patterns the network has to deal with. The network can then be trained completely using prototype points or the training can simply be started using the prototype points and then finished off using the exact data set. Clustering is also used as the starting point for the LVQ family of classification algorithms.
ART stands for Adaptive Resonance Theory , a method of doing pattern recognition and learning using architectures in which the architecture can be described by a set of differential equations and where, when a pattern match occurs, the system ``resonates". ART models are thought to be similar in many ways to how the brain operates. The ART models have been developed mainly by Grossberg and Carpenter and there are two main versions of ART models that have been produced. ART I uses input patterns that consist of only 0s and 1s while the newer ART II can handle analog patterns. Here we will only look at ART I. Whereas the models can, and usually are, described in terms of solving a set of differential equations the weights used in the network converge to well defined values that can be easily described by simple formulas, therefore, instead of describing ART I precisely in terms of differential equations we will just use the simple formulas. A complete description of ART I can be found in [Grossberg 1988a] (chapter 6) A simple description of ART I and related algorithms can be found in [Moore 1989]. A description of ART II can be found in [Carpenter 1987a].

The function of the ART I architecture is to look at patterns and
either categorize them as belonging to a group of patterns it already
knows about or to take a novel pattern and create a new category for it,
thus it is another method of clustering data. The most important parts
of the architecture are shown in figure 11.10. Each node in the R
(for recognition) layer represents a different category that ART can put
patterns in. In operation, a pattern is placed on the I (for input)
layer and then immediately copied onto the C (for comparison) layer.
Between the R and C layers there are weighted connections designed to
activate the units in the R layer. We will call the matrix of these
bottom-up weights, b. Each of the R layer units are activated by the
input pattern in the typical fashion:
|
To make the comparison between the candidate category represented by the unit RJ and the actual input pattern a comparison is made in the C layer. There is an additional set of weighted connections that go from the R layer to the C layer and we will call the matrix of these top-down weights, t. All these weights will be 0 or 1 and they represent the prototype pattern associated with a category. The RJ unit will send activation down its connections to the C layer. Units on the C layer will combine the pattern coming from RJ with the pattern coming from the I layer and will form a new pattern in the C layer. If the pattern formed in C has enough 1 bits in common with the pattern coming from the I layer the input pattern will be accepted as an instance of the category represented by RJ. In particular, if the number of 1 bits in C divided by the number of 1 bits in I is greater than a user chosen parameter, r, the vigilance parameter, then the match is acceptable and the system is said to resonate. When the resonance occurs the top-down and bottom-up weights are modified and the algorithm ends.
However, if the pattern sent down by RJ is not close enough then the reset control becomes active and it strongly inhibits RJ so that it will not become active again during the current search process. Now the pattern I will be copied into C, C will activate a different node in R. This R node will send a pattern down to C and, again, if the pattern coming down from the winning R node is close enough to the pattern coming up from I then the pattern matches. If the match is not close enough the current active R node is strongly inhibited, another R node is selected, etc. If the input pattern does not match any existing node then an unused node will become activated and match the input by default.

To be more specific we will now look at a simple example of how ART
handles the 4 patterns of 25 bits each shown in figure 11.11.
The initial bottom-up weights, bij, start out with the values:
|
When the first pattern is input all the R nodes will light up to
0.21. The nodes compete as to which one gets selected as the winner and
let us assume node 1 wins. Its pattern, the set of weights from R1
to each Ci, is initially composed of all 1s. Now every location in
C that is receiving a 1 from above and a 1 from below becomes 1 while
all the other C nodes become 0. Five out of 5 of the 1s from the input
pattern are matched, this is greater than 0.7, so resonance occurs and
weights in the network are adjusted. The bottom-up weights are changed
to:
|
|
When the second pattern is input node 1 lights up to 1.039604 while the remaining nodes are all approximately 0.38 so node 1 is the winner. Node 1's pattern together with the input from I produce a pattern with only five 1 bits in C. 5/9 is less than 0.7, so node 1 is strongly inhibited by the reset control. Node 2 is selected as the next candidate. It matches 9 out of 9, resonance occurs and the weights are updated as before.
When the third pattern is input R2 has a value of 1.044199 so it is checked first. There are 9 out of 13 matches, a ratio of 0.69 that is less than 0.7, so the search continues. Next node 1 is selected, its value is 1.039604, but only 5 out of 13 matches occur. Finally, node R3 is selected, resonance occurs and the weights are updated.
When the fourth pattern is input, node R3 lights up, there are 13 out of 17 matches, a ratio of 0.76, so the fourth pattern is classified as being in category 3.
If the value for r during the training process had been 0.8 a fourth category would have been created while if the value for r had been 0.2 only one category would have been created. Notice, then, that a low vigilance parameter produces a coarse grouping of patterns and a high vigilance parameter produces a fine degree of discrimination.
In general it may take a number of training passes for a network to learn all the patterns. Any given training pattern may be coded first in one category and later, in another pass, in another category. Once the categories have stabilized any member of the training set will be placed in the correct category on the first try.

The Learning Vector Quantization algorithm, version 1, (LVQ1) is a
nearest neighbor algorithm where some prototype points for each class of
pattern are moved around to try to maximize the probability of correctly
classifying data. The first step in LVQ1 is to take data from each
class and apply a clustering algorithm (such as the one in section 11.3
or possibly a more sophisticated one) to create a set of prototype
vectors. Now for a training set data point, ti, find the
prototype point, pn that is nearest to it. If pn
classifies the point correctly then move pn closer to ti
using the formula:
|
|
As an example2 we take the same training and testing data used in the DSM test in figure 3.7?. First, 12 prototype points, 7 from class A and 5 from class B, were generated using the 1000 training points and the clustering algorithm in section 11.1 with l = 0.1, 0.05 and 0.025 in three passes and a close enough distance of 5.0. These 12 initial prototype points gave a correct classification of 92.9% on the testing set of 1000 points. Then LVQ1 was applied using a = 0.1, 0.05 and 0.025 in three passes through the algorithm. This improved the classification to 95.4% on the test set.
As noted in section 3.2 the LVQ algorithms are new and so far they have been used less than back-propagation. Geva and Sitte [Geva 1991] show that DSM is better and faster than LVQ1 or back-propagation on some test cases but they note that the LVQ algorithms may be better on problems where the training set contains probabilistic errors or fuzzy class boundaries.
The counter propagation networks of Hecht-Nielsen [Hecht-Nielsen 1987], [Hecht-Nielsen 1988] were each designed to be a kind of self-programming look-up table with some ability to interpolate between its table entries. They are therefore useful for doing approximations of real-valued functions. There are two versions of the network, the general version and the feed-forward version. The general version of the network has 5 layers and inputs are made on both the first and fifth layers. Processing flows both up and down and this counter flow of activation in the general version of the network is responsible for the name, counter propagation. We will look at the feed-forward version first and then the general version.

The feed-forward version of counter propagation resembles the nearest neighbor and RCE networks. The description we use here comes from [Hecht-Nielsen 1988]. A sample feed-forward counter-propagation network designed to compute sin(x) is shown in figure 11.13. This network has three layers and as with a back-propagation network, each layer can have as many units as necessary. To use a network once it has been trained, a pattern is placed on the input units, this pattern activates the middle or Kohonen layer which then activates the output or Grossberg layer.
Training the network is done in two phases. The goal of the first phase of training is to find a set of weights for the lower portion of the network that correspond to points in space that are highly representative of the training data. This makes this part of the process very similar to simple clustering. In the second phase, the upper level weights are modified to try to give the correct answer. All the weights are started out with some small random values.
In the first phase of training a pattern is placed on the input layer
and each unit in the Kohonen layer computes the Euclidean distance from
the point it represents to the pattern on the input layer. Whichever of
these middle layer units has the smallest value wins and becomes 1,
while all the other middle layer units become 0. If we designate the
values of the middle layer units as a vector, z, and call the
winning unit, i, then zi will be 1 while all the other zj, j
¹ i, units will be 0. Because this unit, i, responded strongly
to this particular input and it is therefore kind of naturally suited to
recognizing this pattern, the weights leading into it are altered so
that the next time the same pattern is presented, unit i will be even
closer in terms of distance to this pattern. If we let the input unit
values be a vector, x, of n components then the weight,
wpi, from an input unit p to unit i is altered according to the
formula:
|
The training of the weights between the second and third layers is
similar to the above. Patterns are input and one middle layer unit will
become active while all the others stay off. Let the desired values of
the output units be the vector, y, of m elements, then the
weight, uik from the winning middle layer unit, i, to the kth
output unit is altered according to:
|
Unfortunately, it is not always easy for the network to find a set of weights that are representative of the data set. The result is that the network may get stuck and therefore be unable to learn some of the input patterns. This is equivalent to a back-propagation network getting stuck in a local minimum. One proposal for dealing with these problems is to add random noise vectors to the training set. Another is to keep track of how often each middle layer unit wins the competition and then a unit that wins too often should be disqualified occasionally and a runner-up unit should be chosen as the winner instead.
After the training stage has been completed, the operation of the
network is slightly different. Whereas in training, only one unit
in the middle layer was selected as the winner, now, more than one unit
can be allowed to partially win. The sum of the values of the winning
nodes must total 1.0. With more than one winner in the middle layer
each of the winners will contribute to producing an output value so that
the output will be a blend of the output features of all the chosen
winners. In effect, the network interpolates between the values it was
trained on. It is up to the user to find a good way to select and
weigh the influence of the middle layer nodes that are closest to the
input. One very simple scheme might be the following. Suppose after
computing the distances of the input point from each middle layer unit,
it turns out that the three closest units had the values:
|
|
|
|

We now take a look at the general version of the counter propagation network using the description from [Hecht-Nielsen 1987]. In this description, all the inputs are normalized vectors. The network consists of five layers as shown in figure 11.14. Inputs are made in layers 1 and 5. The pattern, x, goes on layer 1 and its answer, y, goes on layer 5. Inputs from both these layers serve to activate the units in the middle layer, layer 3 and their values will be represented by the vector, z. These middle layer units activate units in layers 2 and 4. Layer 2 will produce a y¢ vector that is an approximation for the value of y and layer 4 will produce a vector x¢ that is an approximation for the x value. In operation, you can supply the network with x or y or parts of both x and y and the network will supply the missing parts.
To train the network, you start with small random values for the
weights, however, some sets of weights must be unit vectors (see below).
When a pair of values, x and y are placed on layers 1 and
5, they activate units in the z layer according to the formula:
|
|
|
The same weight modification scheme is used to modify the weights
used to produce the patterns y¢ and x¢. If we designate
the weights from layer 3 to layer 2 as wij, and the weights from
layer 3 to layer 4 as tij, then the weights are changed according
to:
|
|
After training, the outputs x¢ and y¢ are formed by blending together values from the winning nodes in the z layer, as in the feed-forward version.
Bidirectional associative memories (BAMs) come in several different varieties the simplest of which is the Hopfield network that stores single binary patterns. The next more complicated variety stores pairs of memories and it is this variety we will look at in this section. Beyond this variety, however, there are some more complex versions as well, which we will simply mention.

The most common variety of BAM stores pairs of binary associations. There are two sets of units in the BAM, one for each of the pair of patterns. We will call these two sets of units, A and B. They do not have to be the same size. In figure 11.15, we show a BAM network and two pairs of data. The first pair of memories is the letter A and its ASCII code and the second pair is the letter Z and its ASCII code. When a pattern is placed on the A layer, its matching pair will eventually appear on the B layer but it will normally require a few iterations before the pattern stabilizes. Likewise, a pattern placed on the B layer will eventually produce the matching pair on the A layer.
The memories for the BAM are placed in a matrix in a manner virtually
identical to the method we described for the Hopfield network. A
difference is, however, that instead of coding the patterns as binary
(0/1), they are coded as bipolar (-1/1), thus all the 0s must be
replaced by -1s. If the A layer bipolar pattern is x and the B
layer bipolar pattern x is associated with is called y,
and there are k pairs of patterns, then to create the matrix, m, of
weights between the A and B layers, the inner product of each pair of
bipolar row vectors (x and y) is created and added
together:
|
Recall of memories can be done several ways. During recall, the
pattern placed on either set of units is binary and not bipolar. When a
pattern is placed on one layer of the network, the units can update
asynchronously according to the following equations:
| |||||||||||||||||||
| |||||||||||||||||||
In the type of BAM we have been describing, units take on the discrete values 0 or 1. Continuous BAMS have units that take on continuous values from 0 to 1 and the equations describing the values of the units are differential equations. In addition, continuous BAMs can use other learning rules, where the weights are gradually altered to form the weight matrix. These BAMs are known as adaptive BAMs (ABAMs). BAMs implemented in optics are possible. For more on BAMs see [Kosko 1987] and [Kosko 1988].
| 11.1. |
| 11.2. |
| 11.3. |
| 11.4. |
| 11.5. |
| 11.6. |
1The RCE network algorithm has been patented by Nestor, Inc., Providence, Rhode Island. Readers are warned that patented algorithms cannot be used in programs without an arrangement with the owners of the patent.
2Again, results vary depending on all the parameters and random values involved.